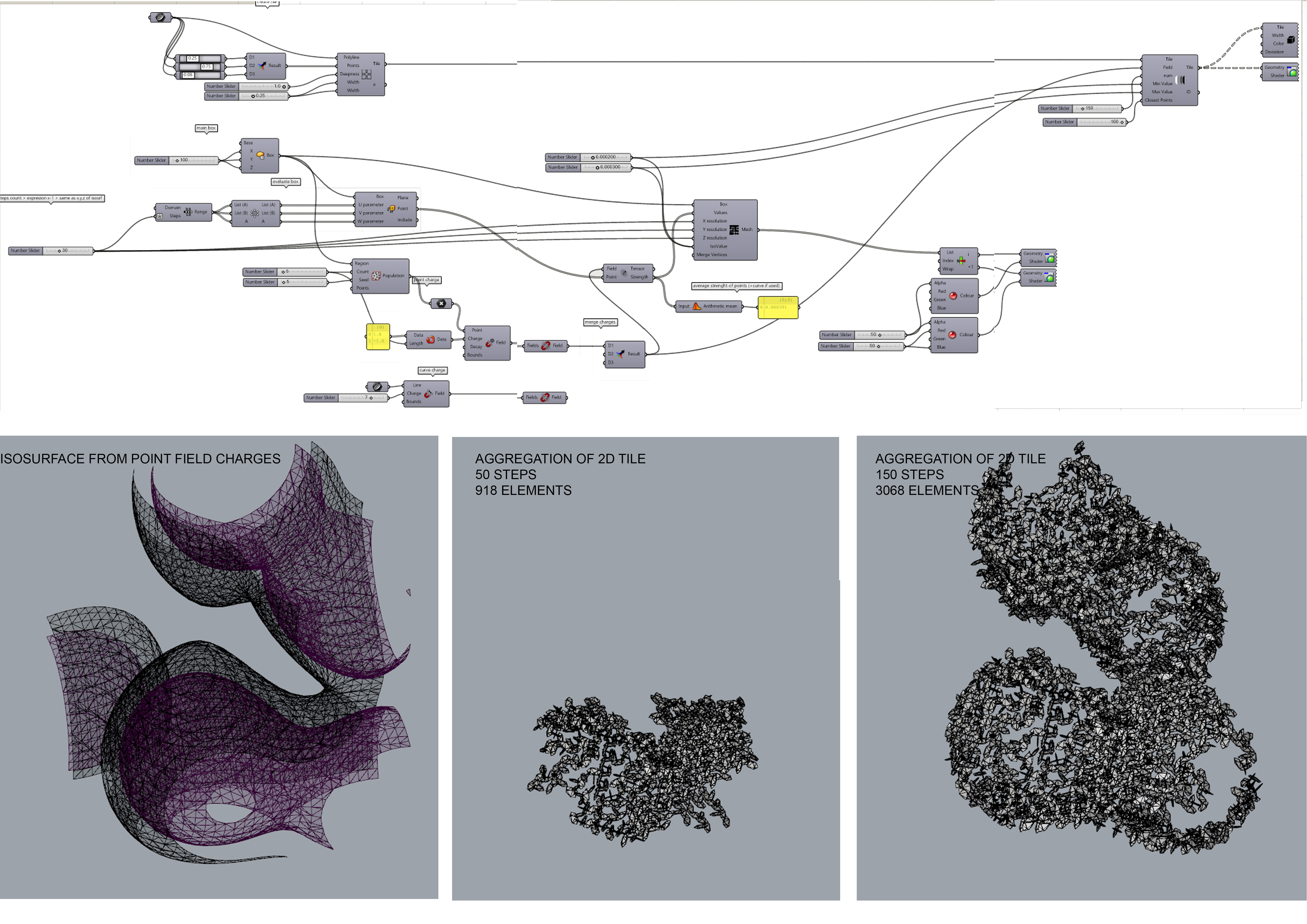
Maybe someone will find it useful or interesting. Another definition of tile aggregation I made learning Fox plugin for grasshopper.
Studio 9: Architectural Notations
KTH Royal Institute of Technology Architecture School
Maybe someone will find it useful or interesting. Another definition of tile aggregation I made learning Fox plugin for grasshopper.

Maybe someone will find it useful or interesting. Another definition of tile aggregation I made learning Fox plugin for grasshopper.


By looking at structures in nature there is a tendency to form a regular 2D or 3D grid from basic shapes. Going back from small scale into a large scale by slight “mistake“ in structure of the grid the whole shape or volume of the object is becoming irregular.
In the beginning of the project I started to look at several Platonic and Archimedean solids by joining them together and exploring the characteristics and composition of volumes (combining cuboctahedron and cube into aggregation the composition had some rhythmic and static behavior while combining icosahedron the volume and the shape was mostly irregular and unpredictable). Therefore for further development of the project I have chosen icosahedron as lattice structure for the research of the geometry inside by individually defined rules.
Some fragmented pictures of final physical model:


Grasshopper definition:
1 step – icosahedron geometry from weaverbird icosahedron:
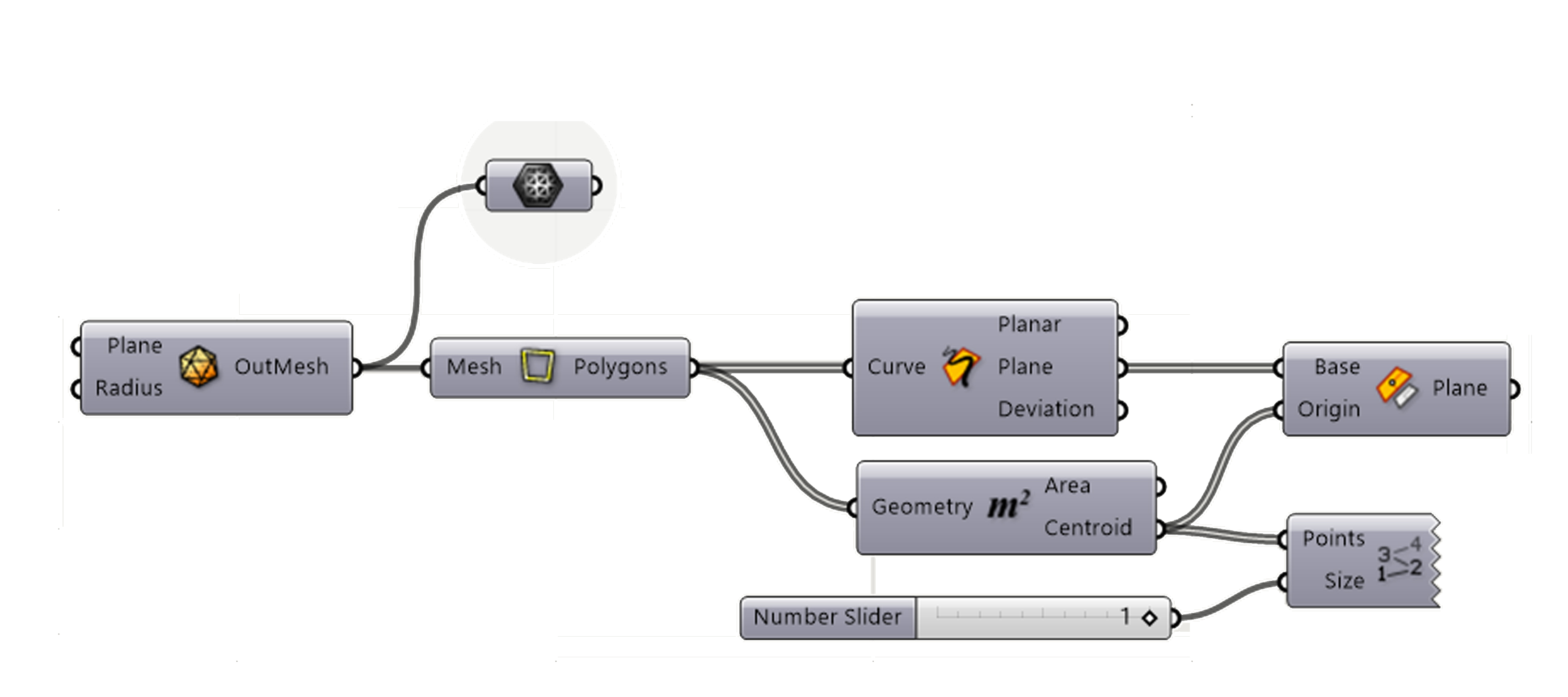
2 step – designing a detail inside the icosahedron frame using kangaroo relaxation:

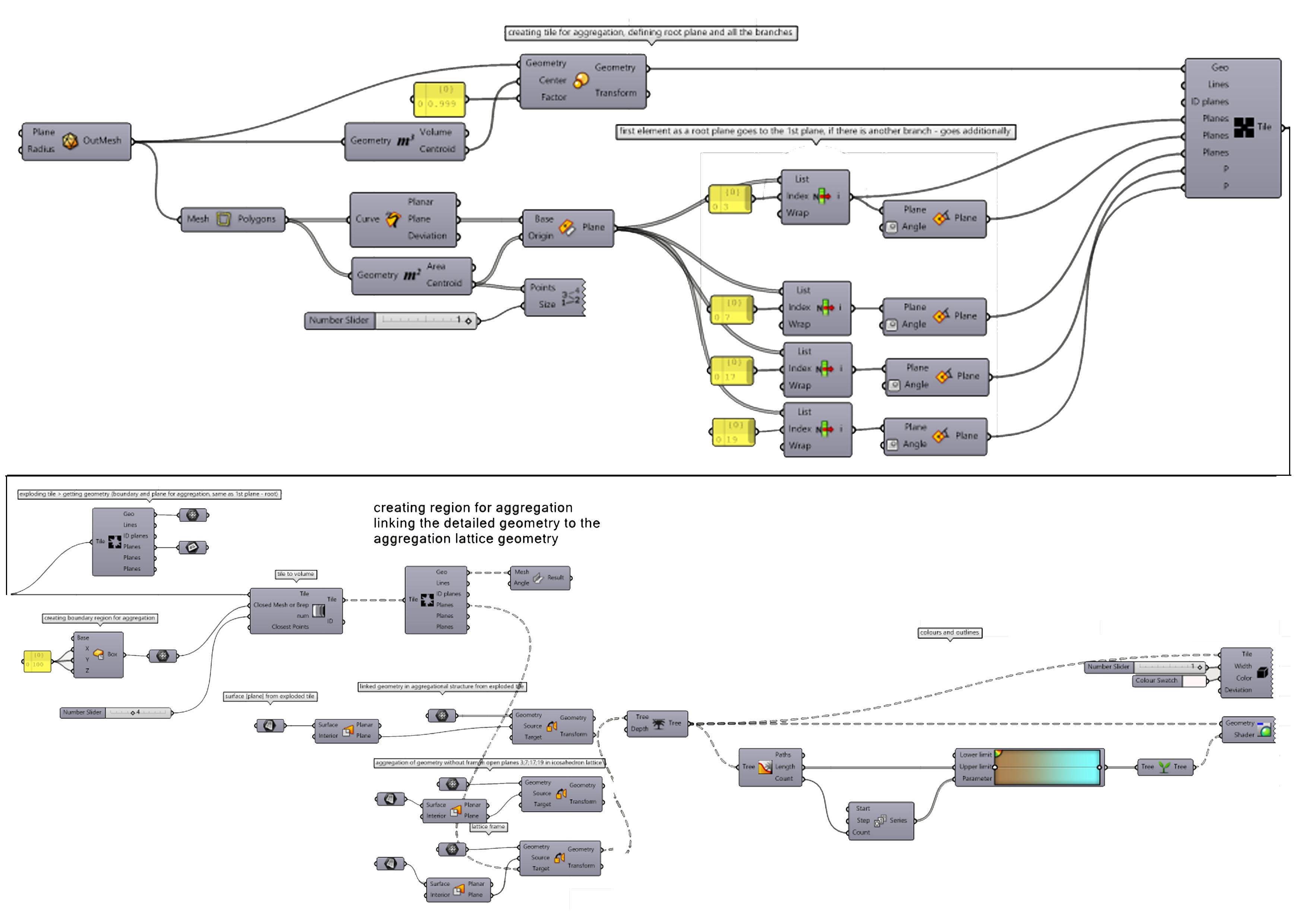
3 step – creating aggregation of icosahedron lattice structure using fox plugin:
Posters of project:
Thanks to tutors and guest critics for accurate comments! And it was fun (not easy at all) to make first steps in the new field of unknown.
Work progress together with assignment_02
Going deeper exploring simple platonic/archimedean solids having them as a frame/lattice structure in which different kind of geometry can be created. Trying to find/define the rules for creating continous space and/or different geometry.
Learned how to create tilling patterns, morphing definition, mesh relaxation in kangaroo and some aggregations with Fox plugin, trying to combine aggregations with a mesh relaxation.
An alternative plugin for aggregations to wasp plugin [works a little faster but only with 1 same repetitive element].
Download link: http://www.food4rhino.com/app/fox
An investigation into how triply-periodic minimal surfaces are defined, derived, and classified. Includes description of examples known in 1972. Plateau’s problem. Fundamental concepts of the differential geometry of minimal surfaces, including the Schwarz reflection principle; Euler characteristic; mean curvature; Gaussian curvature; Gauss map of a surface by parallel normals onto the Riemann sphere; associate and adjoint surfaces; skeletal graphs; complementary minimal surfaces; the classical Schwarz surfaces and the gyroid.
Part 1: https://www.youtube.com/watch?v=JulrXPr19hs
Part 2: https://www.youtube.com/watch?v=-9bB00XShWQ
Part 3: https://www.youtube.com/watch?v=bokgQhFoMjY
Part 4: https://www.youtube.com/watch?v=3APTe-VubOI