‘Flat pieces cost one dollar, single curvature pieces cost two dollars, double curvature pieces cost ten dollars. The good thing about the computer is that it allows you to keep a close control over the geometry and the budget.’ – F. Gehry
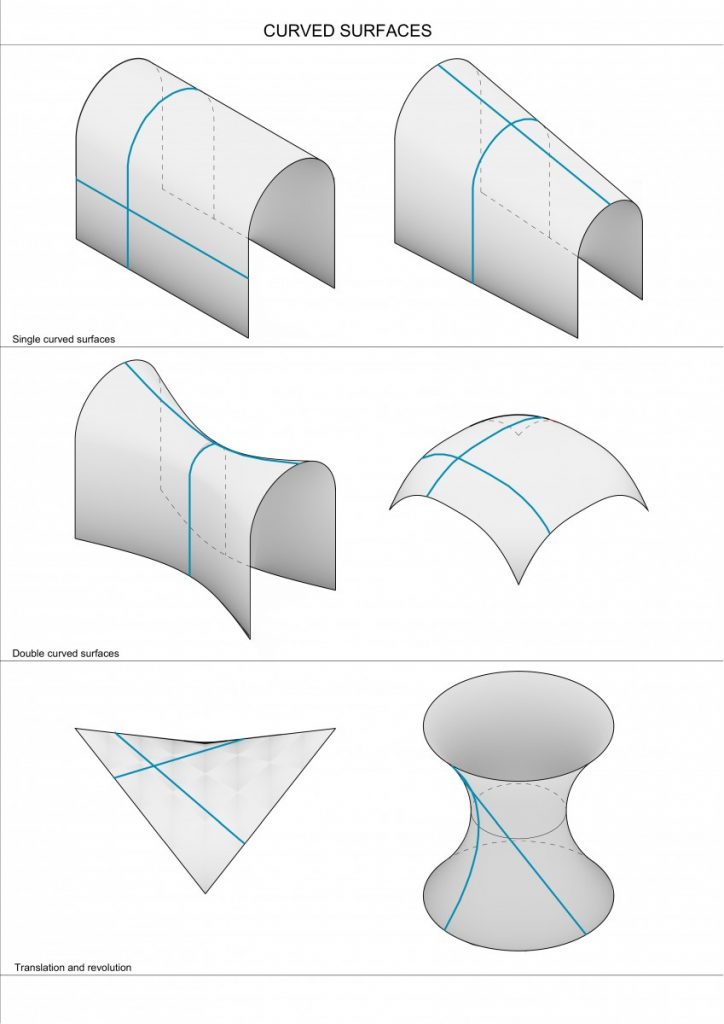
Single Curved Surface – only one of two curves is actually curved, making this shape developable (in mathematics, a developable surface is a smooth surcafe with zero Gaussian curvature, meaning it could be flattened on plane without distortion).
Double Curved Surface – non-developable surface. Saddle shell has compressive stresses along the convex curvature and tensile stresses along the concave curvature. In the 2nd dome example when both dimensions are curving in the same direction meaning that the dome is under compression everywhere.
Hyperbolic paraboloid is a double curved shape which can be created with straight lines, yet non-developable. Both hyperbolic and conical paraboloids has excellent tensile and compressive properties and can be built with straight members, that making the production relatively cheap and easy.
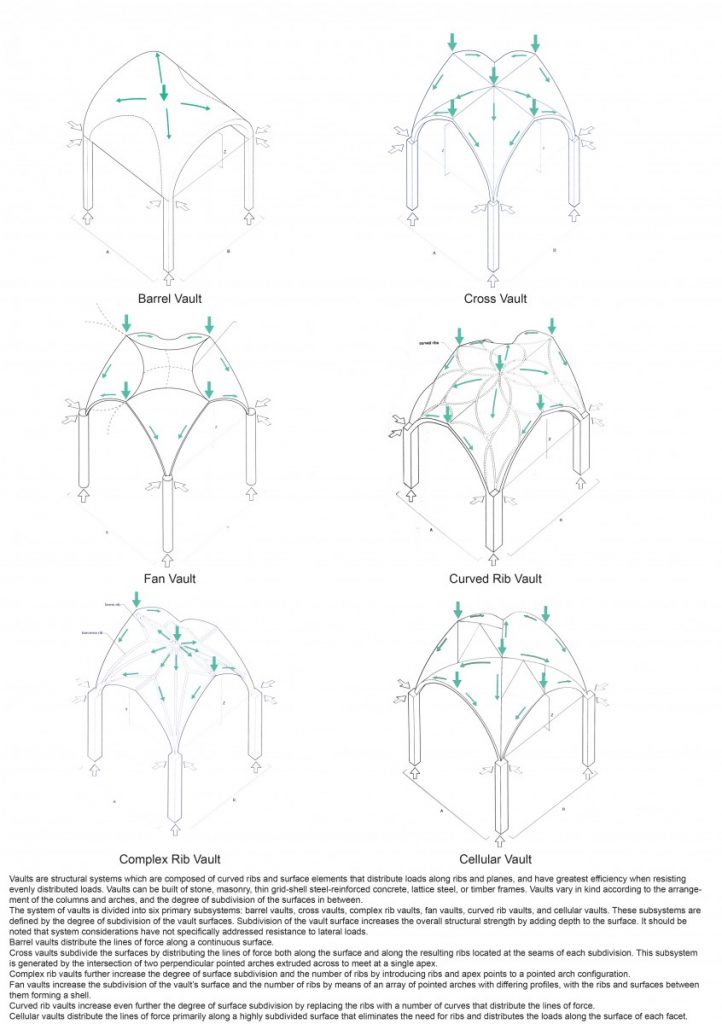
Vaults are structural system which are composed of curved ribs and surface elements that distribute loads along ribs and planes, and have greatest efficiency when resisting evenly distributed loads. Vaults vary in kind according to the arrangement of the columns and arches, and the degree of subdivision of the surfaces in between.
Can be divided into 6 primary subsystems defined by the degree of subdivision of the vault surfaces.

There are many great examples of vault architecture built in the mid-centuries, mostly used for sacral building. For the most of these examples building process took even several centuries. Most of them were arranged as a tessellation of the same symmetrical element, although even then some elements in the building system were trying to break the symmetry.


In the works of E. Dieste we can find the same repetition of symmetrical elements, thus making the production easier, cheaper and faster.
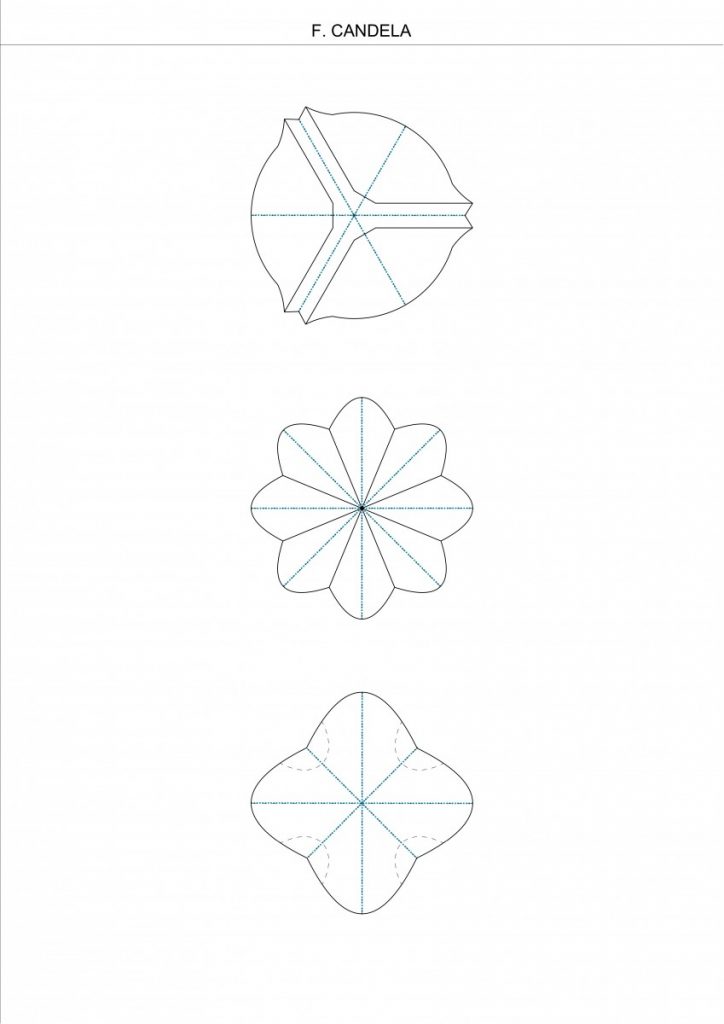
In the F. Candela’s approach we can find radian symmetry and repetition of the same element.
Same as vaults, shells are composed of surfaces that distribute loads in plane and have the greatest efficiency when resisting evenly distributed loads.
Going forward to present:

Block Research Group (BRG) for the past 10 years are researching both shell and masonry structures of double curved surfaces. Due to the computational and digital fabrication tools being able to break the symmetry and work with free form structures.
In 2016 at Venice Biennale presenting the Armadillo vault project, which was built from flat stone pieces, without any glue/cement, meaning that structure was compression-only based.
There I want to discuss two different types of joints – the structural and the holding or orientational ones (such as mortise tenon joint). Structural joints – such as found in Frei Otto buildings or Japanese temples are the elements which basically holds all the structure and loads, meaning that without them it is destabilized and without equilibrium, meaning that they are extremely expensive and complex.
When the structure is in equillibrium itself – meaning it is stable by itself, the joint ensures the stability of it according to the external factors, such as wind, earthquake, explosions, hurricanes. For the long-term structures such joints was cement or grooves, sometimes both of them.
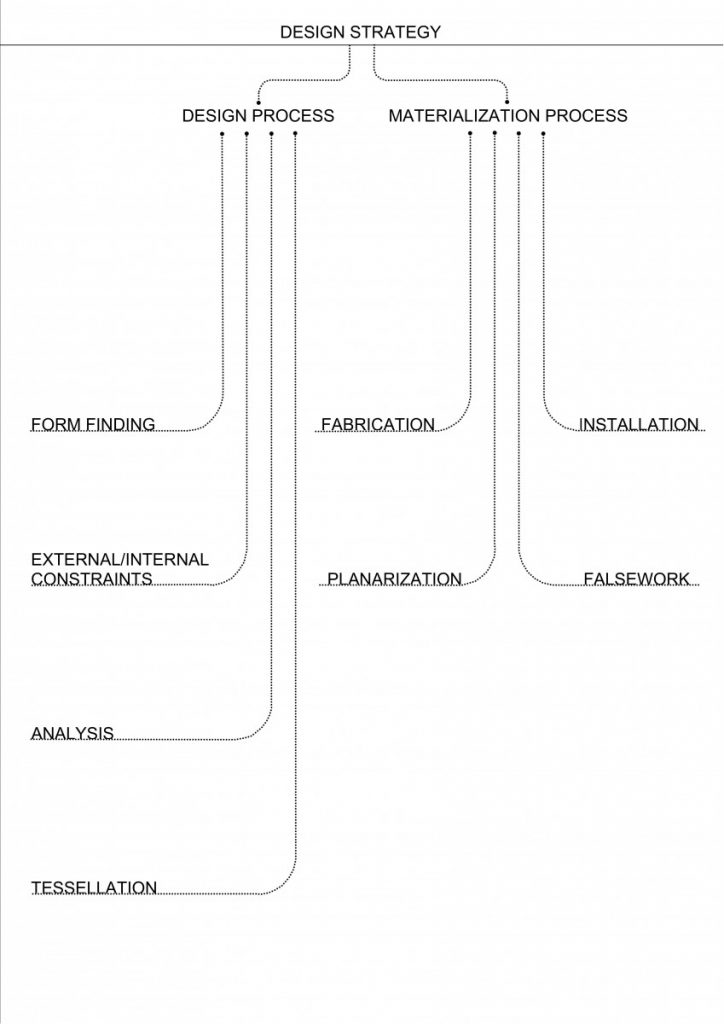
The primary approach for the design strategy in this project was based on BRG research methodology, where it consisted of two main stages – design and materialization. Design consisting of form finding, which can be influenced by external or internal constraints (such as – terrain, sunlight, the size and width with height or openings defined by the architectural program, function, vistas, flows (as movement).
And structural analysis with tessellation of a shell.
Production is mainly consisting of two main parts – fabrication and installation.

During the background research I was working with two different plugins – Kangaroo2 by D. Piker for grasshopper and RhinoVAULT by M. Rippmann for Rhino5, the detailed workflow comparison of both of them can be found in the image above.

As both experiments with the structures made with Kangaroo2 and RhinoVAULT failed I was able to formulate further research development, defining these main parameters:
- Sliding moment or in other words – angle between two elements;
- Tessellation pattern;
- Thickness of elements;
- Orientational joint design;
- Planarity of elements (meaning that touching surface is reduced by element’s shift during the planarization);

And decided to change 1 thing at the time.
… And experiment failed again.
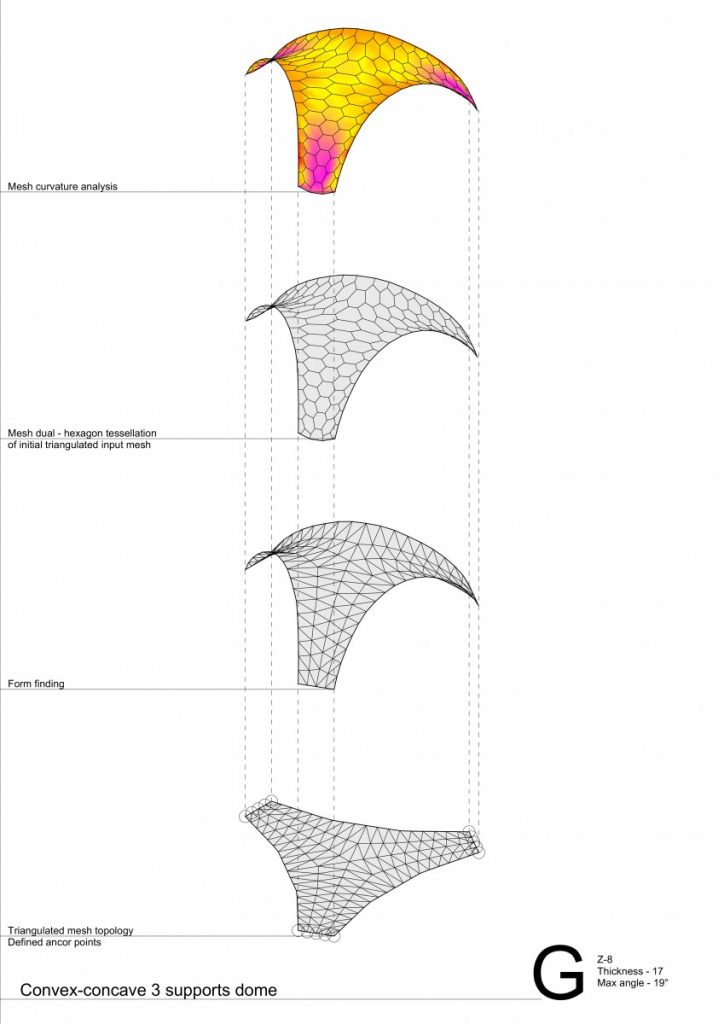
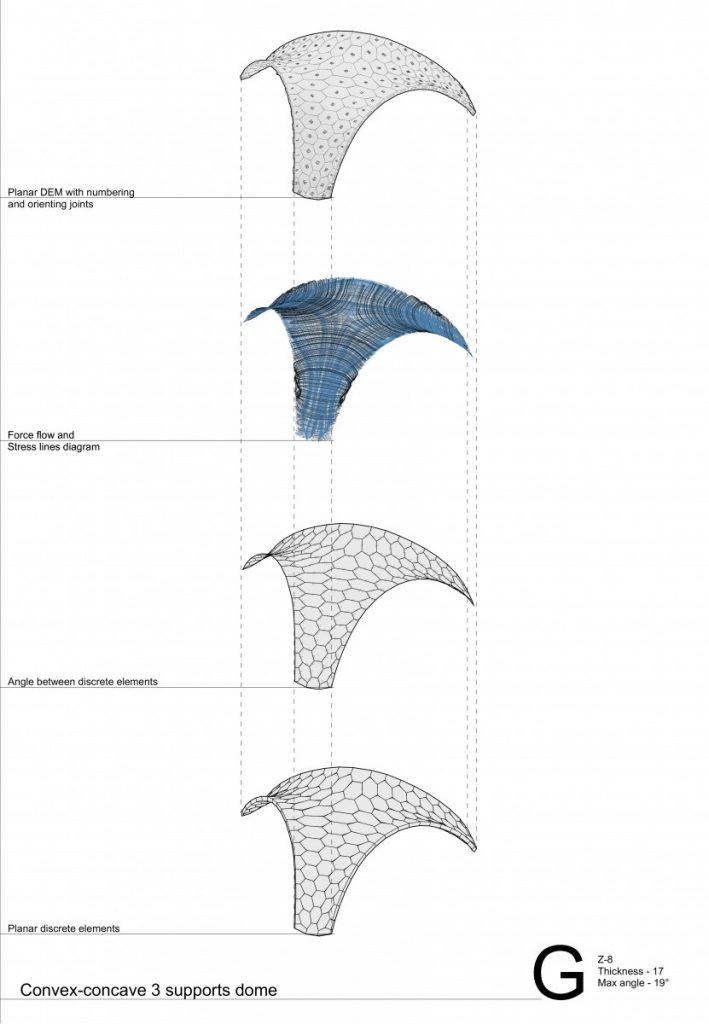

All that helped me to develop my own research methodology – making things clear – to start from simple things, such as arches, where I could test the impact of curvature degree and thickness.
And gladly, this time that worked.
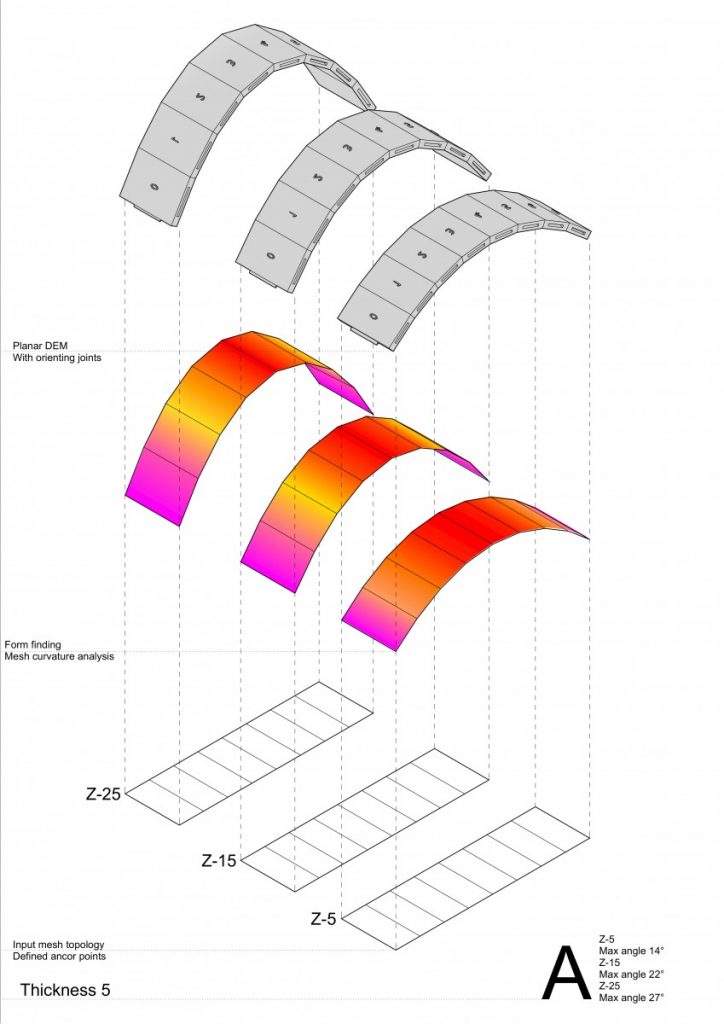
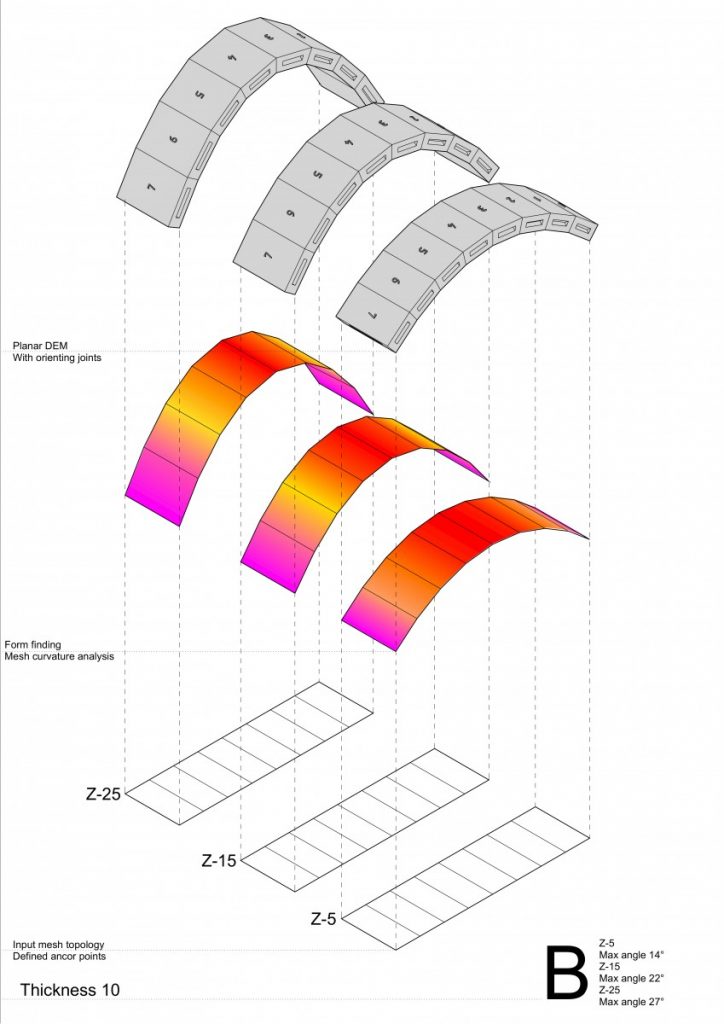
Where I could make clear conclusion about the matter of thickness not so much of a curvature degree.
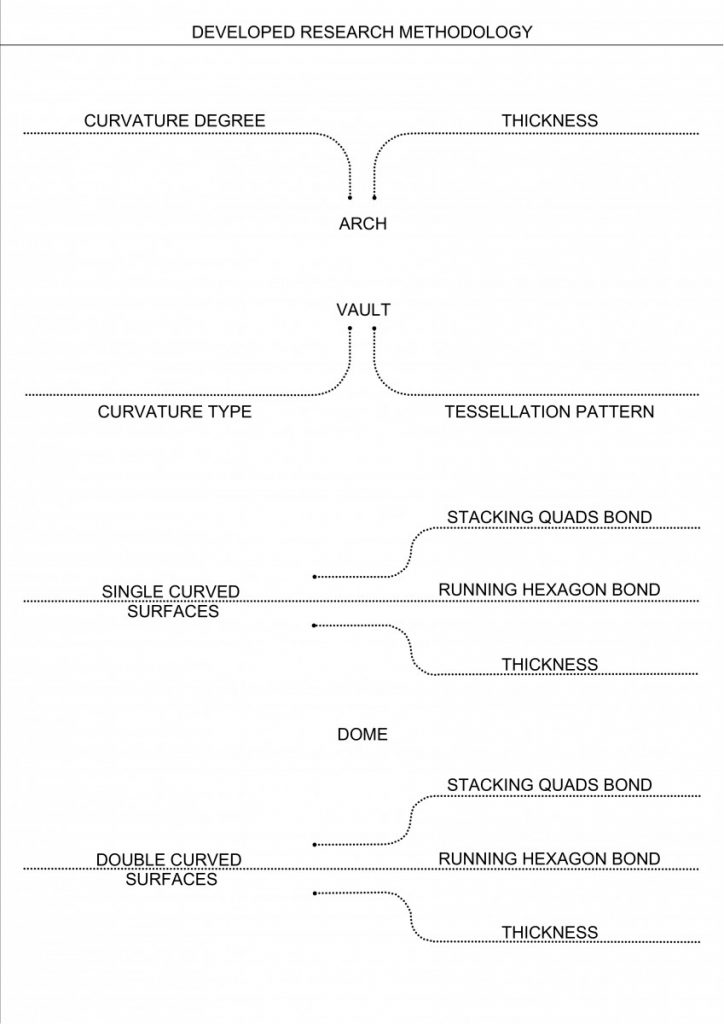
Moving forward to add two new variables – curvature type and tessellation pattern testing in it on more complex geometry – vaults.
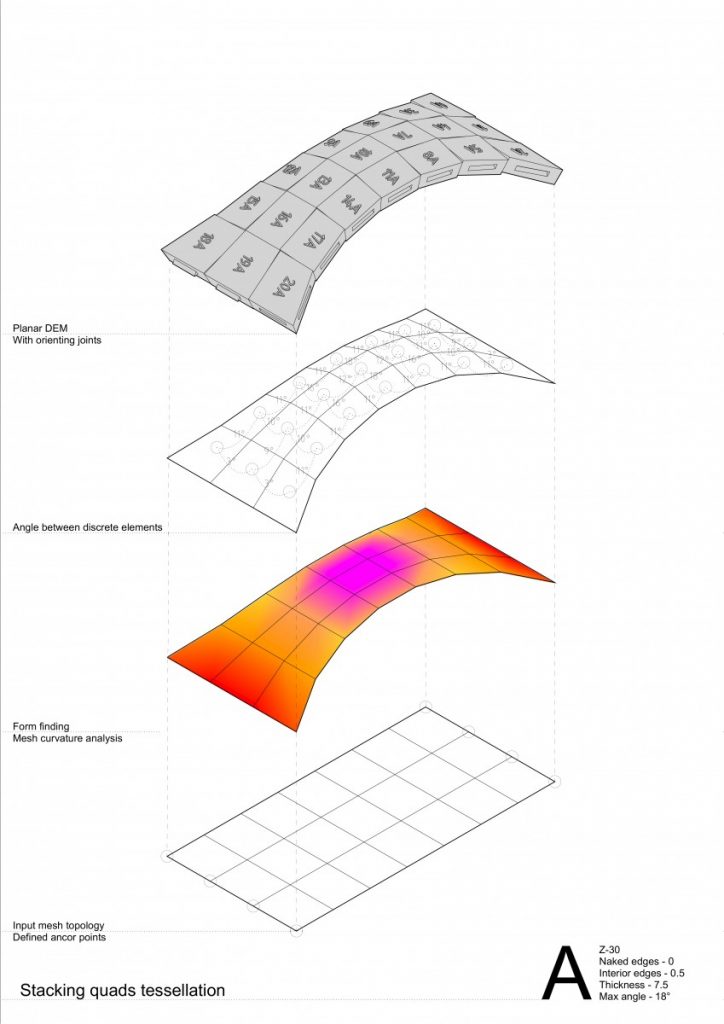
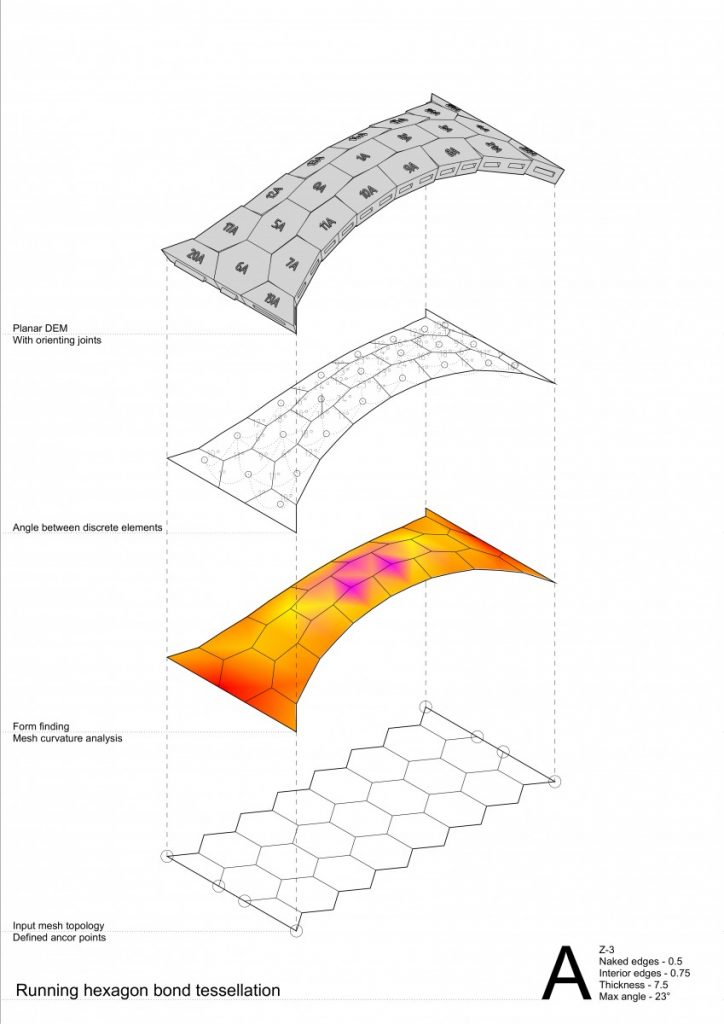
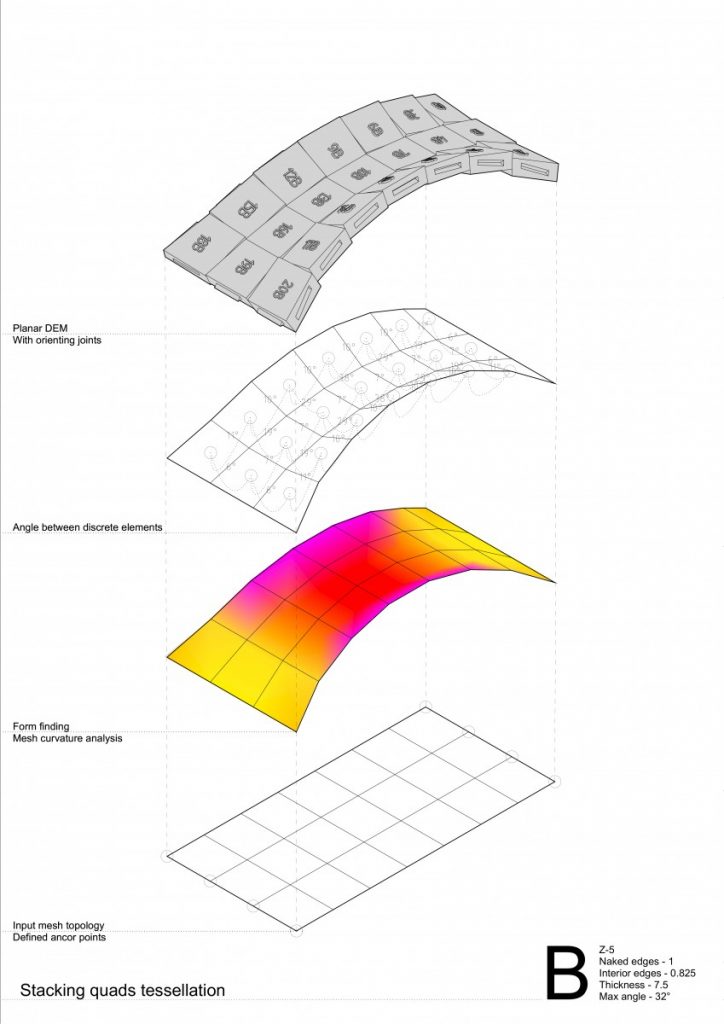
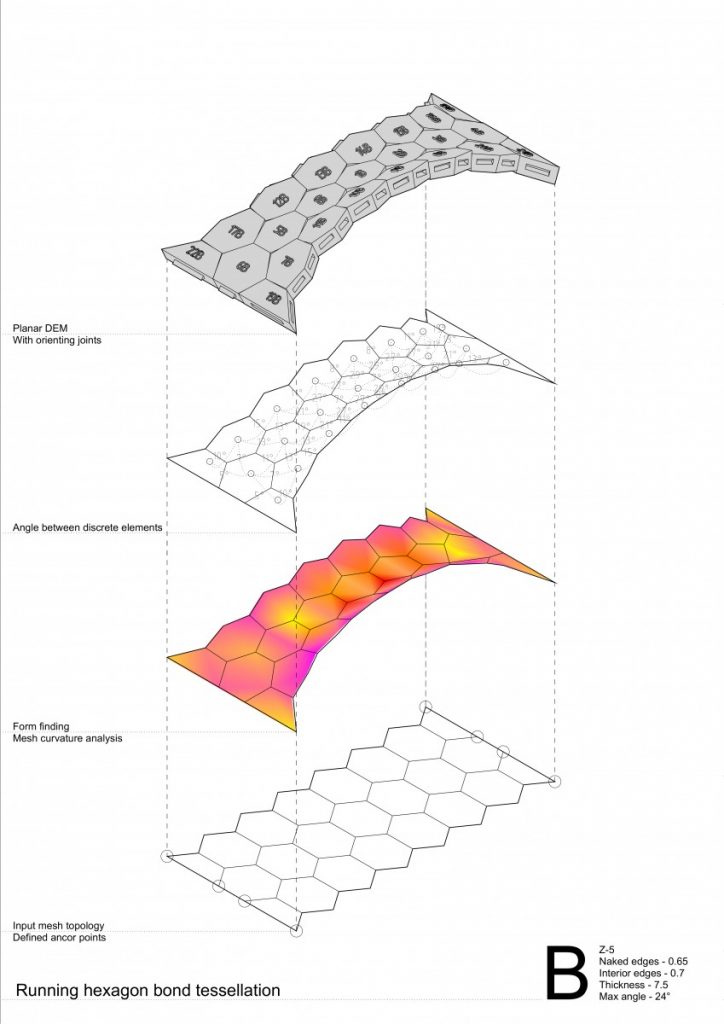
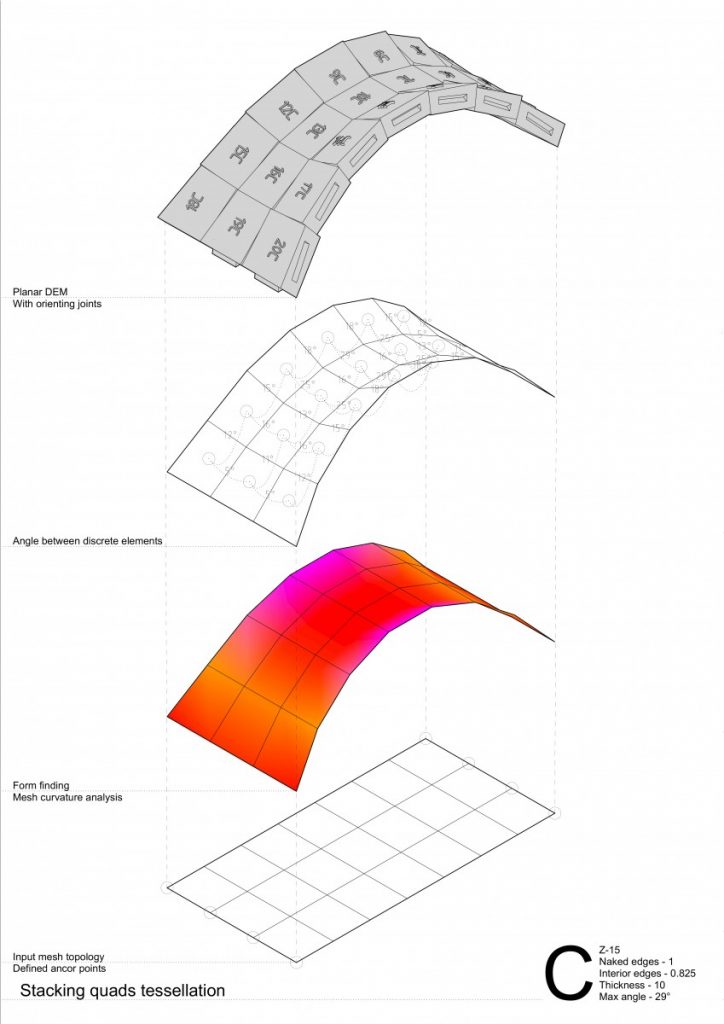
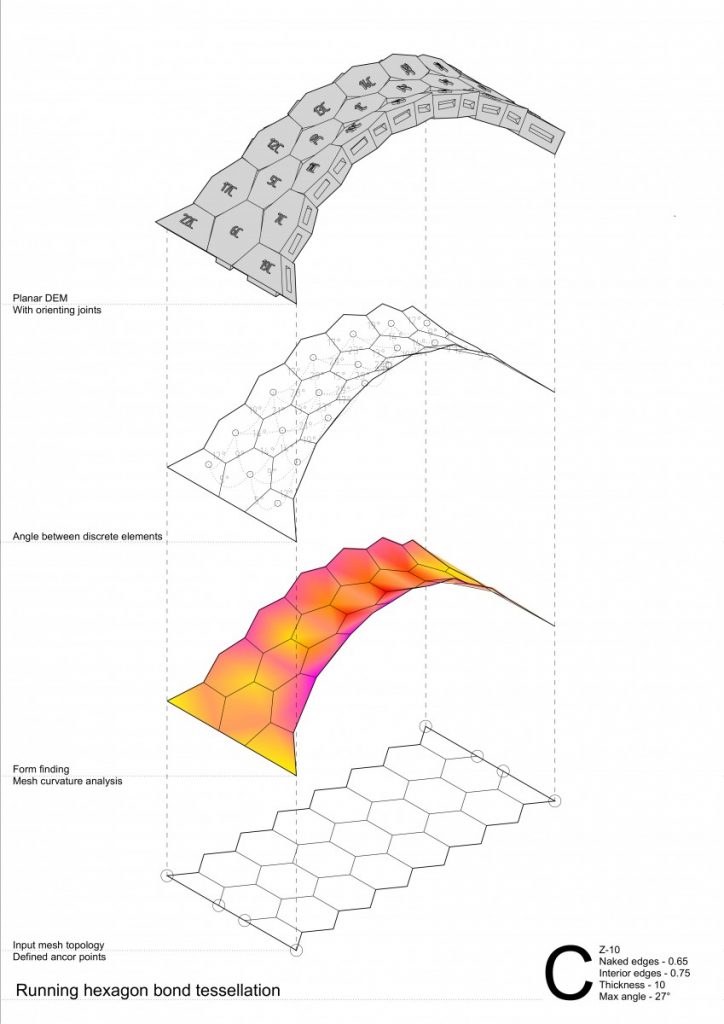
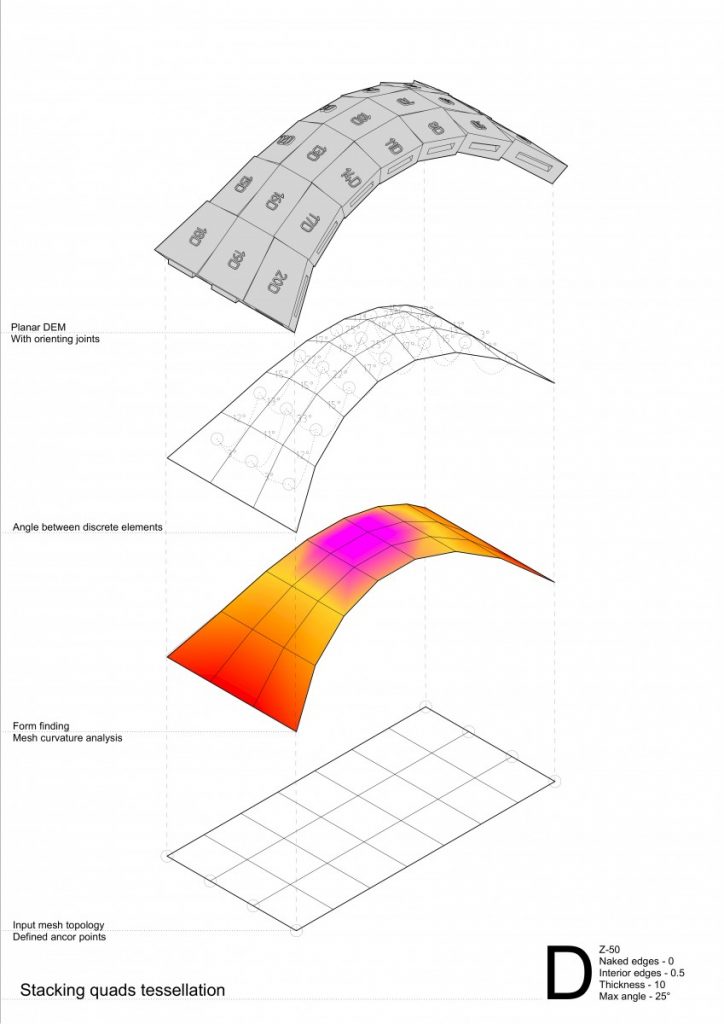
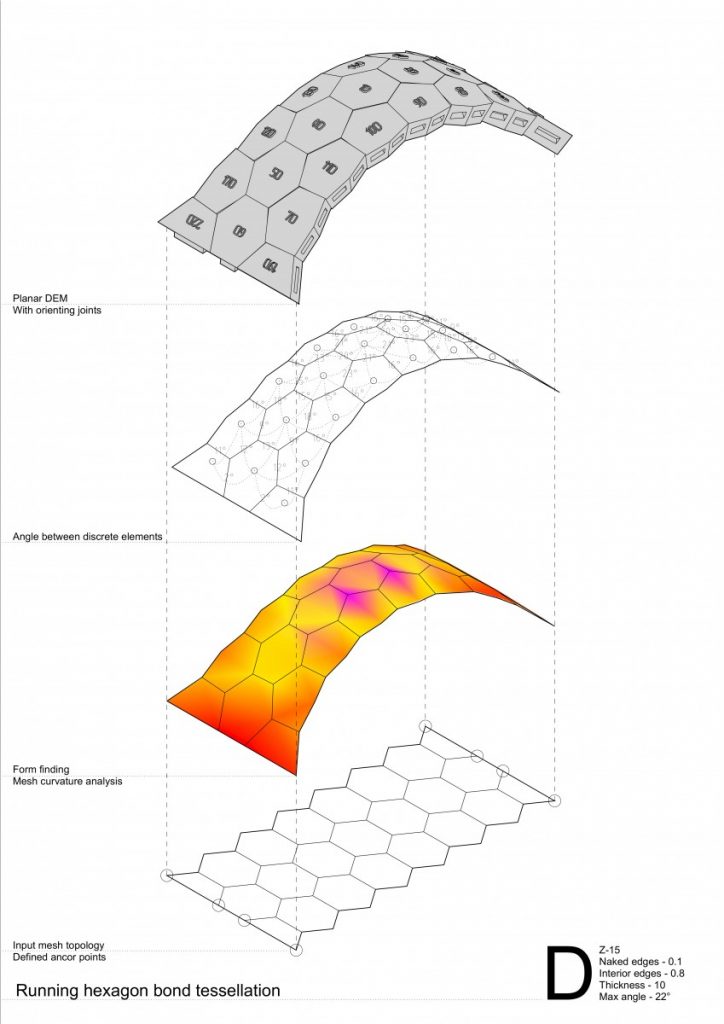
The conclusions made from these series of experiments were:
- Running hexagon tessellation has greater behavior of a self interlocking elements;
- In convex curvature stripes tend to separate from each other by arches both in stacking quads and running hexagon bond tessellation;
- While in concave – convex curvature by forces coming from the side stripes the problem disappears;
- Higher degree of curvature or in other words angle between elements has an impact of greater behavior of a compression-only based structures;
- Hexagon tessellation in concave curvature tends to higher distortion thus becoming more similar to a quad. If the concave curvature would be even higher – hexagon with tends to have two opposite corners going inside the 2D geometry (reminding a ribbon shape);
And to move even more forward – testing single and double curvature with variables such as tessellation pattern and thickness on even more complex geometry – domes.
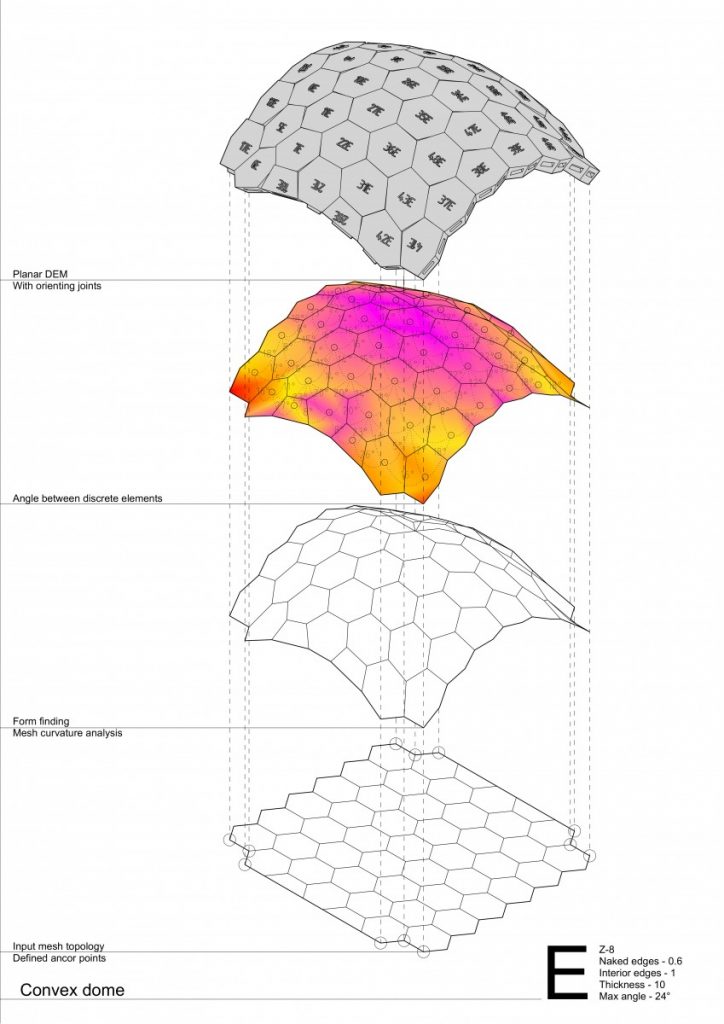
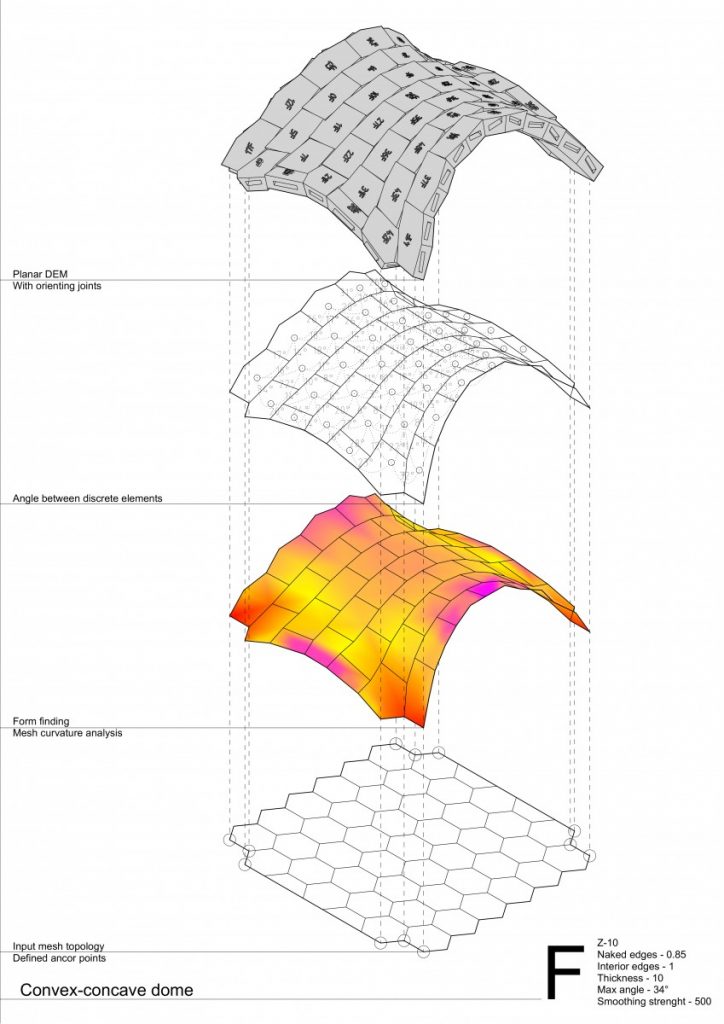
- In convex running hexagon tessellation the self interlocking behavior of a pattern feels even stronger, the structure is extremely stable, comparing to all other experimental models.
- While convex-concave stripes tend to separate themselves into individual arches, although the structure is stable and distribute even loads very well, able to carry 20x of it’s self weight (doesn’t work for a point loads at all…)

As the production strategy in this project is equally or even more important than a design process I would go through key points:
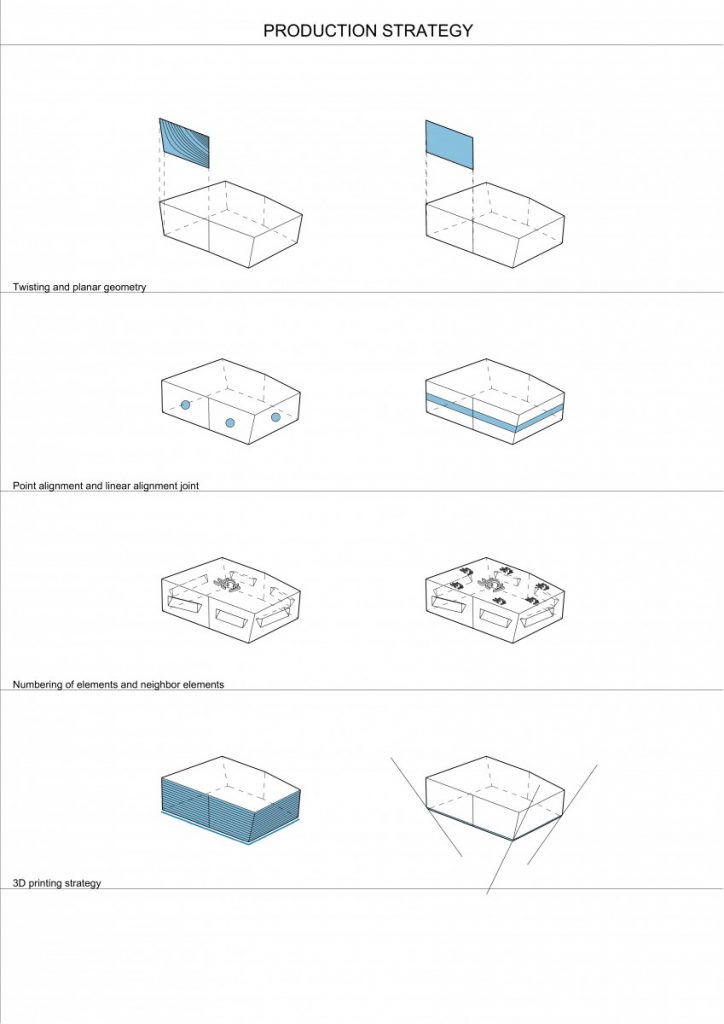
- Twisting and planar geometry – rapid and easy production is impossible having twisting geometry, therefore discrete elements needs to be planar and 3D printable or easy to cut;
- As from the previous research it was clearly seen that points loads with the radius of 2mm and the height of 1mm are not enough for alignment between elements and due to the sliding moment in between them causing the collapse of the entire structure they were improved to linear alignment joints;
- All elements are numbered, but this part could be improved by defining the neighboring elements’ numbers, thus making the assembly possible without any additional instruction;
- As for the 3D printing strategy – challenges found there consist of tolerances, shrinkage and expansion of the material, so called elephant’s foot at the bottom of the element – all these can be solved by testing, trying and experimenting with your machine. As for the elephant’s foot – chamfering the bottom edges of the elements worked pretty well.
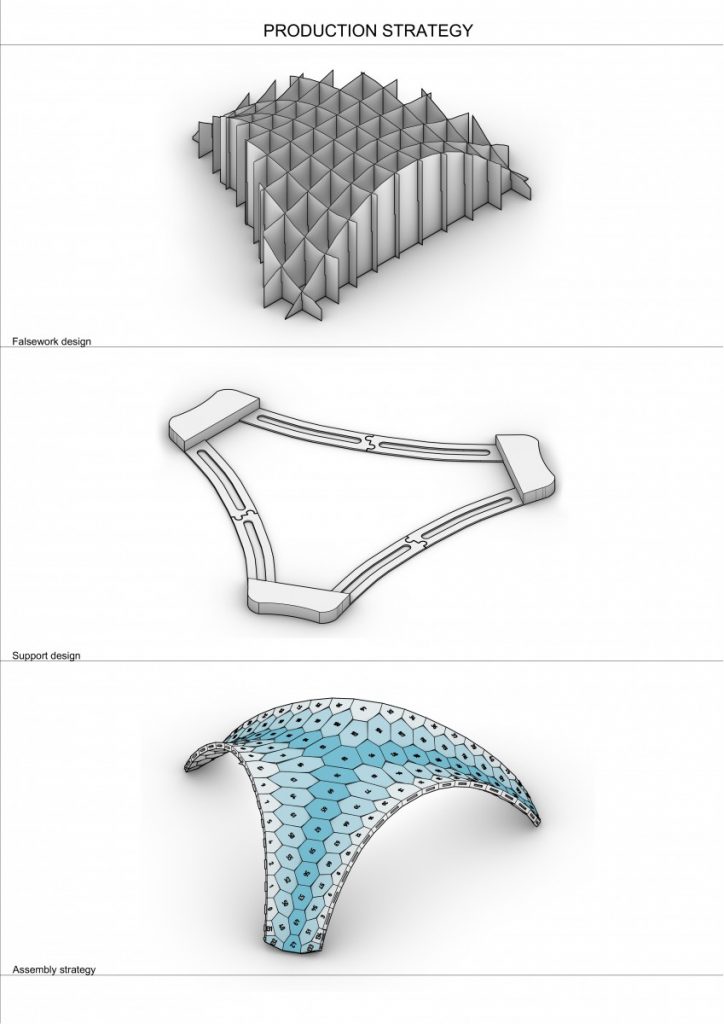
Falsework is made using Bowerbird plugin for grasshopper making it fast and easy both for the design and production.
Supports are modeled manually, but also evolving during the whole research – tolerances, joining separate parts of support structure, reducing mass for faster production, design etc.
Assembly strategy – working with smaller structures helper to very easily and intuitively understand the principle of going by stripes/arches and from medial spine while assembling the structure.
To sum everything up, my objectives during this master thesis project is to develop a deeper understanding in the structural behavior of free form structures based on the scientific research method – learning by observation – meaning that infinitely strong digital clay model in digital environment should be tested as a physical model.
Be able to work with complex systems, investigate the possibility of adaptivity of shell structures to different terrain conditions, therefore the shift between the bespoke design and the universal design model.